안녕하세요 여러분! 오늘은 딥러닝에 대해 얘기를 해보겠습니다 ㅎㅎ
여러분들이 관심을 가지고 있든 없든 '딥러닝' 이라는 것에 대해 얘기를 한번 쯤은 들어보셨을 것입니다.

(출처 http://dongascience.donga.com/news.php?idx=10850)
지난 2016년에 있었던 세기의 대국! 인공지능 알파고와 이세돌 선수의 대국에서, '딥러닝' 기술을 활용한 알파고가 4승 1패로 이세돌 선수를 이겼던 기억이 있죠 ㅎㅎ
이때부터 언론에서 인공지능에 대해 다루는 일이 많아지고, 저처럼 인공지능 분야에 관심을 가지게 된 사람들이 많았을 것이라 생각이 됩니다.
그 외에도 요새 너무나도 핫한 자율주행, 인공지능 스피커, AI 면접관 등 정말 다양한 산업군과 분야에서 이 인공지능이라는 키워드를 자주 다루고 있습니다.
★여기서 잠깐!! 지금 제가 인공지능이라는 말과 딥러닝이라는 말을 번갈아 사용하고 있었던 것을 눈치 채셨나요?
사실 굉장히 많은 사람들이 인공지능과 딥러닝이라는 단어를 잘 모르고 사용하고 계신 경우가 정말 많은데,,, AI를 전공하는 입장으로서 정말 마음이 미어진답니다...
하지만 이 글을 읽고 있는 우리는 이 개념들이 무엇인지 제대로! 알고 사용해보도록 해요 ㅎ.ㅎ
인공지능 vs 머신러닝 vs 딥러닝
우리가 흔히 이 단어들을 통용해서 사용하지만, 조금 더 엄밀히 말하자면 이들은 조금 다른 의미들을 가진 단어입니다.

(출처 https://blogsabo.ahnlab.com/2605)
위 그림이 아마 인공지능과 딥러닝의 관계를 잘 나타내주는 그림이 아닐까 싶습니다.
인공지능을 구현하기 위한 방법의 하나로 머신러닝이 있고, 딥러닝은 이 머신러닝 방법론 중 하나의 종류인 것입니다!
- 인공지능이란 말 그대로 인공적으로, 컴퓨터를 통해 지적 능력을 구현하는, 좀 더 개념적인 단어를 의미하고,
- 머신러닝은 컴퓨터가 '학습' 을 통해 스스로 그 성능을 향상 시키는 방법론을 의미하며
- 딥러닝은 인간의 뉴런을 모티브로 한 '인공신경망' 방식을 바탕으로 컴퓨터를 학습시키는 것을 의미합니다.
사실 '인공지능'이라는 개념은 조금 모호한 개념이라고 생각됩니다. 어디까지가 '지능'을 닮아있고, 어디부턴 아닌지가 조금 알쏭달쏭하기 때문이죠 ㅎㅎ
주차장에 있는 번호판을 인식하는 기기는 과연 인공지능일까요? 단순한 프로그램일까요? 저는 잘 모르겠습니다

(출처 http://smarcom.biz/ko/license-plate-recognition-system/)
머신러닝부턴 조금은 명확해집니다. Machine (기계) + Learning (학습), 즉 기계가 스스로 학습하게 하는 방식을 의미합니다.
어떤 데이터들을 컴퓨터에게 줬을 때, 컴퓨터는 그 데이터들을 통해 다양한 방법으로 '학습'이라는 것을 하게 되고, 이 학습이라는 것을 기반으로 지능을 흉내낼 수 있게 됩니다.
보지 못했던 새로운 데이터를 만났을 때, 학습된 컴퓨터는 학습 결과를 바탕으로 어느정도 예측을 할 수 있게 되는 것이죠
(만약 모든 경우의 데이터에 대해 어떻게 동작할지 컴퓨터에게 알려준다면, 이는 컴퓨터가 학습은 하지 않았지만 어느정도의 인공적인 지능을 가진 것 처럼 보일 수 있겠죠? ㅎㅎ)
딥러닝과 인경신경망
그렇다면 딥러닝은 과연 어떤 것일까요?
★딥러닝은 여러 비선형 변환기법의 조합을 통해 높은 수준의 추상화를 시도하는 기계 학습 알고리즘의 집합 - 출처 위키백과
정의를 보면 조금 어려운 것 같긴 합니다 ㅎㅎ..
딥러닝에 대해 더 알아보기에 앞서, 이해를 돕기위해 '인공신경망' 이라는 개념에 대해 잠시 알아보겠습니다.

(출처 http://tcpschool.com/deep2018/deep2018_deeplearning_intro)
위 그림은 인공신경망을 검색하면 나오는 대표적인 그림인데요! 어디선가 한 번 본적 있는 것 같지 않나요? ㅎㅎ
위 그림에서 '층'(입력층, 은닉층, 출력층) 으로 표현되어 있는 것은 '데이터'라고 생각하시면 될 것 같습니다.
예를 들어 맨 왼쪽의 녹색 입력층은 말그대로 입력되는 데이터를 의미하고, 맨 오른쪽 출력층은 이 신경망에서 출력되는 데이터 (결과) 라고 생각하시면 될 것 같습니다. 그리고 은닉층은 계산 과정에선 쓰이지만 실제로 사람이 직접 잘 다루지는 않는, 숨어있는 (hidden) 층이라고 생각하시면 될 것 같습니다.
위의 예시에서 입력층의 경우 다섯개의 노드(점) 으로 이루어져있는데요, 이는 5개의 원소로 이루어진 데이터라고 생각하시면 됩니다. 예를 들어 (1, 1, 2, 0, 1) ← 이런 벡터도 여기에 당연히 포함되겠죠?
★한 층은 하나의 데이터를 의미하고, 노드(점) 하나는 데이터의 요소 하나를 의미함
그렇다면 과연 저 선들은 어떤 것을 의미하는 것일까요?
설명을 위해 왼쪽에서 두번째 층, 노란색 층의 다섯번째 노드(점) 하나를 예시로 들어봅시다!

위 그림은 노란색 노드 하나를 확대한 그림인데요, 확대된 그림에서의 $x_1$ 부터 $x_n$ 은 바로 이전 층, 즉 이 경우엔 입력층의 데이터들이 됩니다. (그렇다면 여기서 $n = 5$ 에 해당하겠죠?)
그리고 점끼리 연결되어 있는 각 엣지 (선) 들은 $w$와 $b$ 라는 요소를 가지고 있습니다.
이들은 각각 weight 과 bias 라는 의미를 가진 요소들이고, 이는 퍼셉트론의 핵심적인 요소입니다!
하나의 결과 노드에 대해 다 같은 값의 bias $b_5$ 를 사용합니다! *즉, 이 경우엔 결과로 얻게되는 은닉층의 노드가 7개가 있으니, 첫번째 층의 계산에서는 총 7개의 bias 값이 존재합니다 ($b_1, ... , b_7)$
위 그림에서 $x_1$ 이라는 데이터는 $w_1, b_1$ 을 가지고 있는 선을 지납니다. 그리고 이 과정에서 weight은 데이터에 곱해지고, bias는 더해집니다. 이 것이 무슨 말이냐면
$x_1 w_1 + b_1$ 이라는 값을 가지고 다음 노드(노란색)에 도착하게 됩니다.

그렇다면 위에서 예시로 들었던 노란색 노드는 이렇게 계산되어 들어오는 값이 다섯개가 있겠죠? (입력층이 다섯개의 노드로 이루어져있음)
그 후, '합'이라고 써져있는 것과 같이 weight과 bias에 의해 계산된 요소들이 전부 더해집니다.

여기서 n 은 5에 해당하겠죠?
그 후 마지막으로 '활성함수'에 해당하는 activation function을 통과하며 퍼셉트론의 계산을 마치게 됩니다.
★이 때 activation function은 한 층에 존재하는 모든 퍼셉트론들에 대해 같은 function을 사용하는 것이 일반적입니다!
*즉 예시로 사용중인 노란색 은닉층의 값을 얻기 위한 모든 계산에서 다 같은 activation function을 사용함
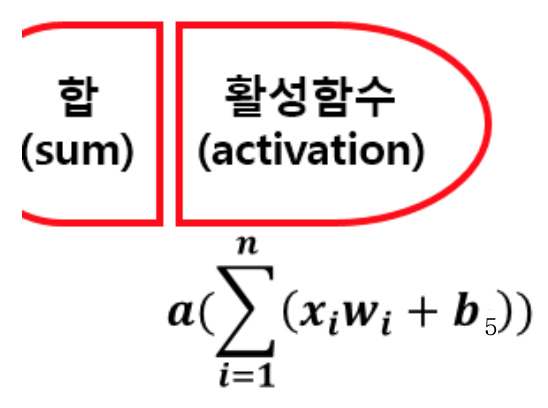
★하나의 엣지 (선) 는 weight과 bias, 그리고 활성함수라는 요소를 가지고 있다.
★weight은 입력으로 들어온 데이터를 어느 정도 비중으로 가져갈지, bias는 데이터와는 독립적으로 어느 정도의 값을 더해줄 지, 활성함수는 엣지에 의해 계산된 결과를 어떻게 활성화시켜 (변환시켜) 다음 층으로 넘겨줄지를 결정한다.
(weight, bias, 활성함수라는 개념은 필요에 의해 만들어진 것으로, 각각이 실제로 어떤 의미를 가지고 있는지에 너무 깊게 고민은 안하셔도 괜찮습니다!)
위의 인공신경망 예시에서 두번째 층에 해당하는 노란색 층 (hidden layer) 은 총 7개의 요소를 가지고 있습니다.
위의 계산 과정을 통해서 나오는 것은 이 일곱개의 요소 중 하나의 노드에 대한 계산이었고, 즉 위와 같은 계산을 일곱번 진행하면 노란색 층 하나에 대한 계산이 완료되는 것입니다.
이 과정을 반복하여 노란색 층에 해당하는 은닉층 (hidden layer) 을 거쳐, 최종적으로 출력층 (output layer)의 값을 얻을 수 있게 되는 것입니다.
그리고 위의 예시는 퍼셉트론들이 다중으로 쌓여있다는 뜻에서 다중 퍼셉트론, Multi-Layer Perceptron (MLP) 라는 이름으로 불립니다. 이는 인공신경망의 종류 중 하나라는 것을 기억해주시면 좋겠네요 ㅎㅎ
그렇다면 이 퍼셉트론이라는 것은 도대체 무엇일까요?
혹시 사람의 뇌에 존재하는 '뉴런'이라는 것을 들어본적이 있으신가요? 저도 자세히는 모르겠지만 뉴런은 서로 연결되어 존재하며 일련의 신호를 전달하고 처리하는 역할을 합니다.
그리고 퍼셉트론 (perceptron) 은 사람의 뇌에 있는 뉴런을 컴퓨터에서 구현한, 즉 인공적인 뉴런이라고 생각하시면 될 것 같습니다.

그리고 이는 위에서 설명한 것과 같이 weight (w), bias (b), activation (a) 이 세가지 요소로 이루어져있습니다.
지금까지의 내용을 이해하셨다면 이젠 딥러닝이 무엇인지 받아드릴 준비가 되셨을 것입니다.
딥러닝의 '딥(deep)' 이라는 단어는 이 인공신경망에서 층이 깊게 (deep) 쌓인 형태의 딥뉴럴네트워크 (deep neural network, DNN) 로부터 나오게 된 단어입니다.
그럼 다시 처음에 봤던 딥러닝의 정의를 한번 다시 보겠습니다
★딥러닝은 여러 비선형 변환기법의 조합을 통해 높은 수준의 추상화를 시도하는 기계 학습 알고리즘의 집합 - 출처 위키백과
여기서 '비선형 변환기법'이라는 것이 나오는데, 이것이 딥러닝, 딥뉴럴네트워크 (DNN) 을 의미있게 해주는 요소입니다.
아까 인공신경망에 대해 알아볼 때 활성함수 (activation function) 가 그 역할을 해줍니다.
활성함수로 사용하는 함수의 종류에는 Sigmoid, ReLU 등등 여러 종류의 함수들이 존재하는데요, 각 함수에 대한 자세한 설명은 다음 기회에 진행해보겠습니다 ㅎㅎ 아래 그림이 이런 활성함수들의 예시들인데, 참고만 해주시면 될것 같습니다.

(출처 https://22-22.tistory.com/20)
중요한 것은 활성함수로 사용하는 위의 함수들은 모두 일반적인 선형함수가 아닌 비선형함수라는 것입니다!

이 그래프에 해당하는 함수는 우리가 아는 일차함수, 즉 선형함수입니다. (Linear function)
만약 활성함수로 선형함수만 사용한다면, 이는 수학적으로 봤을 때 네트워크에 아무리 여러 층을 쌓더라도 단 한층만 쌓은 것과 동일한 것이 됩니다.
아까 딥러닝의 '딥'이 'Deep' Neural Network (DNN, 딥뉴럴네트워크) 에서 나온 단어라고 했는데, 선형 활성함수만 사용한다면 신경망 자체가 한 층인 것과 동일하기 때문에 '딥'하다고 할 수 없겠죠?
비선형 활성함수는 DNN이 의미가 있게 깊은 층을 가질 수 있도록 해주고, 이는 네트워크로 표현할 수 있는 표현력을 높여주는 효과를 가집니다.

위 그림은 빨간색 점들과 파란색 점들을 분류하기 위한 함수들의 예시입니다.
왼쪽의 경우 선형함수로만 두 점들을 분류할 수 있고, 오른쪽의 경우엔 더 복잡한 함수의 형태로 두 점들을 구분할 수 있게 됩니다.
이런 경우에, 오른쪽의 함수가 왼쪽의 함수보다 표현력이 더 높다고 말할 수 있게 되고, 이것이 딥뉴럴네트워크, 즉, 딥러닝을 통해 분류작업을 학습한 결과라고 생각하시면 될 것 같습니다.
딥러닝은 여러 비선형 변환기법의 조합을 통해 높은 수준의 추상화를 시도하는 기계 학습 알고리즘의 집합 - 출처 위키백과
이 정의에서 말하는 비선형 변환기법이라는 것의 필요성을 이제 이해할 수 있으시겠죠? ㅎㅎ
그리고 이 딥러닝의 예시들로 위에서 말한 다중퍼셉트론 (Multi-Layer Perceptron, MLP) 외에도, 이미지 처리를 위한 컨볼루션 네트워크 (Convolution Neural Network, CNN) 등이 있는데, 이 개념들은 다음 번 글들에서 더 깊게! 다뤄보도록 하겠습니다 ㅎㅎ
오늘 이 글을 통해 인공지능, 딥러닝이 무엇인지, 그리고 딥러닝이 왜 세상의 빛을 다시 볼 수 있게 되었는지 잘 전달이 되었으면 합니다.
읽어주셔서 감사합니다! 다음에 만나용 ㅎㅎ

'입문자를 위한 AI 개론' 카테고리의 다른 글
| Overfitting과 Underfitting (0) | 2021.07.20 |
|---|---|
| 지도학습과 비지도학습이란 무엇일까요? (0) | 2021.07.20 |
| 인공신경망은 어떻게 학습되는 것일까? (0) | 2021.07.12 |
| 인공지능(AI) [머릿말] (0) | 2021.07.05 |




